I - Cas d'une variable qualitative :
| Modalités |
Effectifs |
Fréquences |
% |
| modalité 1 |
n1 |
f1 =  |
f1 × 100 |
| ... |
... |
... |
... |
| modalité i |
ni |
fi =  |
fi × 100 |
| ... |
... |
... |
... |
| modalité K |
nk |
fk =  |
fk × 100 |
| Total : |
n |
1 |
100 |
|
| Modalités |
Effectifs |
Fréquences |
% |
| Célibataire |
30 |
0.200 |
20.00 |
| Marié |
80 |
0.533 |
53.33 |
| Divorcé |
20 |
0.133 |
13.33 |
| Veuf |
20 |
0.133 |
13.33 |
| Total : |
150 |
1 |
100 |
|
(Si la variable est ordinale, écrire les modalités dans l'ordre : modalité 1 < modalité 2 < ... < modalité k).
Graphiques : diagrammes circulaires, diagrammes en barres, ou imagés.
(Les modalités d'une variable ordinale sont toujours placées dans l'ordre).
On visualise ainsi le "poids" des différentes modalités dans la population étudiée.
II - Cas d'une variable discrète
| Valeurs de la variable |
Effectifs |
Fréquences |
% |
| x1 |
n1 |
f1 |
f1 × 100 |
| ... |
... |
... |
... |
| xi |
ni |
fi =  |
fi × 100 |
| ... |
... |
... |
... |
| xk |
nk |
fk |
fk × 100 |
| Total : |
n |
1 |
100 |
|
| Nombre d'appels xi |
Nombre de jours ni |
Fréquences fi |
% fi × 100 |
| 0 |
2 |
0.0208 |
2.08 |
| 1 |
14 |
0.1458 |
14.58 |
| 2 |
23 |
0.2396 |
23.96 |
| 3 |
24 |
0.2500 |
25.00 |
| 4 |
18 |
0.1875 |
18.75 |
| 5 |
9 |
0.0938 |
9.38 |
| 6 |
6 |
0.0625 |
6.25 |
| Total : |
96 |
1 |
100 |
|
x1 < x2
< ... < xk
Graphique : diagrammes en bâtons (en effectifs, fréquences, ou %) pour visualiser
l'allure de la distribution statistique.
Le cumul de proche en proche des effectifs (ou fréquences, ou %) dans l'ordre
croissant permet de connaître le nombre (ou fréquence, ou %) d'observations inférieures ou
égales à chaque xi.
Ce même cumul dans l'ordre décroissant donne le nombre (ou fréquence, ou %) d'observations supérieures ou
égales à xi.
Ces valeurs cumulées servent au tracé de la fonction de répartition "en escalier"
(ou courbe cumulative croissante), et de la courbe cumulative décroissante.
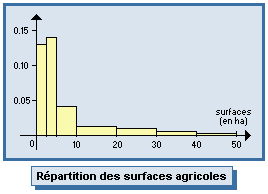
III - Cas d'une variable continue
On découpe l'intervalle des valeurs de la variable en un certain nombre de classes [ ei
ei+1 [ , et on détermine les effectifs ni
associés à chaque classe (ainsi que les fréquences et les %).
Graphique : histogramme.
Le rectangle construit sur chaque classe doit avoir une surface proportionnelle à l'effectif de la classe. On visualise ainsi l'allure de la distribution observée.
Les cumuls se calculent comme dans le cas discret.

Les courbes cumulatives croissante et décroissante représentent le nombre (ou fréquence, ou %) d'observations ≤ , ou > , à une valeur donnée.
Elles sont ici représentées de façon approchée par des fonctions affines par morceaux continues :
Dans certains cas, un diagramme tige-feuilles est aussi possible.