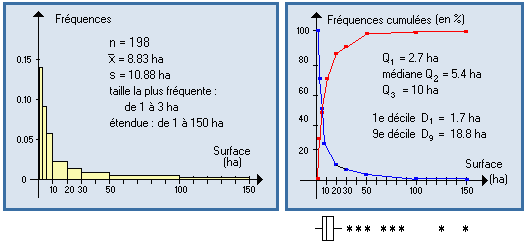
En plus des tableaux et graphiques, on résume l'observation d'une variable quantitative par un petit nombre de paramètres.
I - Tendance centrale
- la moyenne
(arithmétique), éventuellement pondérée
: 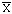
- la médiane : M est insensible aux valeurs aberrantes, mais se prête moins bien aux calculs que la moyenne si le nombre de données est important.
- le mode dans le cas particulier d'une distribution unimodale.
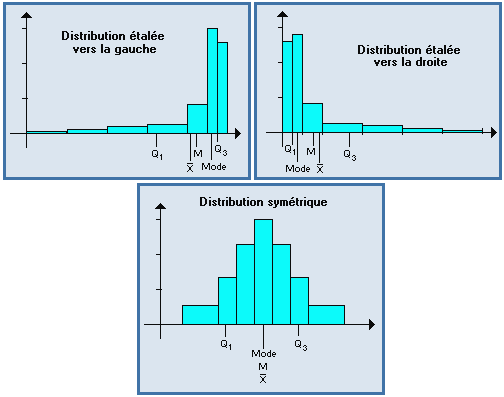
La comparaison de ces trois paramètres donne des indications sur la symétrie de la distribution.
II - Position
- les fractiles (quartiles, déciles, centiles) : ils subdivisent la série ordonnée en un certain nombre d'intervalles (4 , 10 , 100) contenant environ le même nombre de valeurs observées chacun.
III - Dispersion
- étendue
- variance et écart-type : calculés généralement en complément de la moyenne, pour mesurer la plus ou moins grande dispersion autour de celle-ci.
- intervalle interquartile : sa longueur, l'écart-interquartile mesure la dispersion des 50 % valeurs les plus centrales.
- le diagramme en boîte (ou boîte à moustaches) représente les quartiles, et les valeurs extrêmes, en repérant les éventuelles valeurs aberrantes.
| Pour résumer une série unidimensionnelle, il faut toujours la représenter par un ou deux graphiques appropriés, et plusieurs paramètres de tendance centrale, de position et de dispersion. |
L'étude et la comparaison de ces paramètres permet de bien caractériser la distribution, et de repérer d'éventuelles données aberrantes.