Si on dispose de l'observation de
deux caractères, X et Y,
sur les mêmes n individus, on peut, en plus
de l'étude séparée de chaque variable, décrire la
liaison éventuelle entre X et Y.
I - Tableaux et Graphiques
Les données brutes se présentent
sous la forme de n couples de valeurs (ou modalités
).
Si X
et Y sont quantitatives, le graphique approprié
est un nuage
de points.
Si X
est qualitative, et Y quantitative : la distribution
conditionnelle de Y, pour
chaque groupe d'individus associé à une modalité de X,
est représentée par des histogrammes, diagrammes en bâtons
ou en boîtes.
| Catégorie |
Age (années)
|
| A |
32 ; 35 ; 40
; 42 ; 43 ; 43 ; 49 ; 50 ; 55 ; 58
|
| B |
22 ; 26 ; 27
; 27 ; 29 ; 30 ; 31 ; 31 ; 33 ; 34 ; 36 ; 36 ; 38 ; 39 ; 39 ; 42
; 44 ; 46 ; 51 ; 53
|
| C |
20 ; 20 ; 21
; 22 ; 23 ; 24 ; 24 ; 24 ; 26 ; 27 ; 28 ; 28 ; 28 ; 29 ; 29 ; 30
; 32 ; 33 ; 33 ; 35 ; 38 ; 41 ; 43 ; 45 ; 45
|
|
|
 |
Inversement, les profils
des modalités de X, représentés
par des diagrammes circulaires ou en barres, peuvent être comparés
pour les différentes valeurs, ou classes de valeurs, de Y.
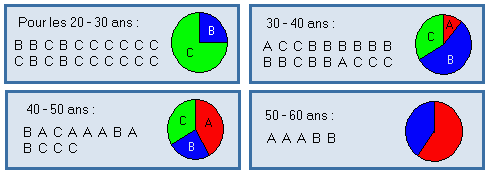
Si X
et Y sont qualitatives, on construit un tableau
de contingence, et on représente par des diagrammes
circulaires ou en barres les distributions conditionnelles de Y
pour chaque modalité de X, et de X
pour chaque modalité de Y.
Les variables discrètes prenant
un petit nombre de valeurs différentes, ou les variables continues dont
les valeurs sont découpées en un petit nombre de classes, peuvent
être traitées pour tous ces tableaux et graphiques comme des variables
qualitatives. Toutefois, les diagrammes en barres ou circulaires doivent être
réservés aux vraies variables qualitatives.
II - Paramètres caractéristiques
 -
Coefficient
de corrélation linéaire : il mesure,
dans le cas où X et Y
sont quantitatives, l'aspect plus ou moins "allongé" du nuage
de points.
-
Coefficient
de corrélation linéaire : il mesure,
dans le cas où X et Y
sont quantitatives, l'aspect plus ou moins "allongé" du nuage
de points.
Il peut se calculer à partir
des données brutes, ou regroupées en un tableau de contingence.
Les moyennes et écarts-types s'obtiennent alors à partir des distributions
marginales.
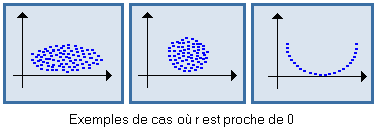
Si r
est proche de 0, X et Y
ne sont pas linéairement corrélées, mais cela ne signifie
pas toujours qu'il n'y a pas de lien entre elles.
Si X
et Y sont ordinales, on calcule le coefficient
de corrélation des rangs de Spearman.
- Rapport
de corrélation entre Y
quantitative et X qualitative (ou assimilée)
: c'est la part de variance de Y expliquée
par X. En effet, la variance de Y
se décompose en :
| variance expliquée |
+
|
variance résiduelle |
| |
| (variance des moyennes par groupe) |
| (moyenne des variances intragroupes) |
- Les courbes
de régression représentent les moyennes
conditionnelles d'une variable quantitative, lorsqu'une autre quantitative est
fixée.
- Le coefficient " "
: calculé sur un tableau de contingence, il est nul dans le cas de l'indépendance
entre X et Y, et d'autant
plus important que les profils sont différents.
"
: calculé sur un tableau de contingence, il est nul dans le cas de l'indépendance
entre X et Y, et d'autant
plus important que les profils sont différents.




 -
-
