LEXIQUE :
Choisissez le terme à expliquer...
Amplitude d'une classe (ou d'un intervalle) :
C'est la longueur de l'intervalle.
L'amplitude de la classe[ei ei+1 [ est ei+1 - ei .
L'amplitude de la classe [ 55 68 [ est 68 - 55 = 13 (unités de mesure)
Une variable statistique est qualitative si ses valeurs, ou modalités, s'expriment de façon littérale ou par un codage sur lequel les opérations arithmétiques telles que moyenne, somme, ... , n'ont pas de sens.
| Exemples : |
|
Une variable statistique est quantitative si ses valeurs sont des nombres sur lesquels des opérations arithmétiques telles que somme, moyenne, ... ont un sens.
| Exemples : |
|
Caractère statistique (ou variables statistiques) :
C'est ce qui est observé ou mesuré sur les individus d'une population statistique.
Il peut s'agir d'une variable qualitative ou quantitative.
| Exemples : |
|
Les centiles C1, C2 , ... , C99 divisent une série statistique en 100 parties d'effectifs égaux.
Ce sont les abscisses respectives des points d'ordonnée 0.01 ; 0.02 ; ... ; 0.99 sur la courbe cumulative croissante.
Par exemple le centile C98 est une valeur dépassée par 2 % des observations ; les centiles n'ont de sens que si on dispose d'un grand nombre (plusieurs centaines) d'observations.
Le centre de gravité d'un nuage de points Mi
de coordonnées (xi , yi)
est le point G de coordonnées ( 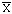 ,
, 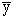 ) ; c'est
le point moyen du nuage.
) ; c'est
le point moyen du nuage.
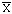 est la moyenne des xi
est la moyenne des xi
et 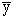 la moyenne des yi
la moyenne des yi
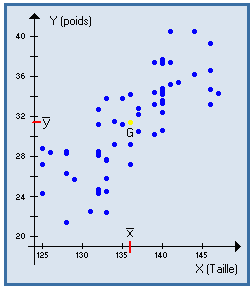
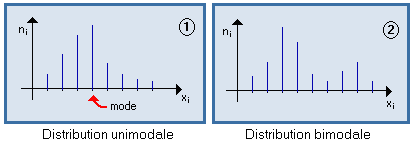
C'est la classe correspondant au maximum de l'histogramme, dans le cas d'une distribution continue unimodale.
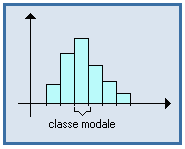
Intervalles de valeurs d'une variable continue, l'ensemble des classes formant une partition de l'ensemble des valeurs possibles de la variable.
Par exemple, si tous les salaires des employés d'une entreprise se situent entre 750 et moins de 3 000 €, on peut construire (par exemple) les classes :
Chaque valeur observée de la variable doit appartenir à une classe et une seule.
Coefficient de corrélation (linéaire) :
Le coefficient de corrélation entre deux variables statistiques X et Y sur les mêmes individus est le nombre :
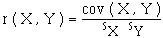
où cov ( X , Y ) est la covariance entre X et Y,
et sX sY les écarts-types de X et Y.
Ce coefficient est toujours compris entre -1 et + 1.
S'il est proche de + 1 ou - 1, X et Y sont bien corrélées, c'est-à-dire qu'elles sont liées entre elles par une relation presque affine ; le nuage de points est presque aligné le long d'une droite (croissante si r = + 1, décroissante si r = - 1). S'il n'y a aucun lien entre X et Y, ce coefficient est nul, ou presque nul.
| Exemples : | 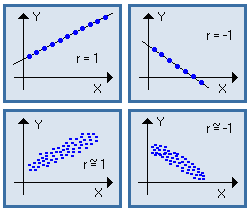 |
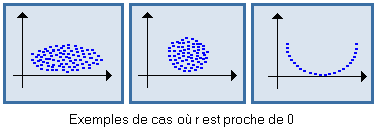 (Voir plus de détails dans le module "Ajustement Linéaire") |
Coefficient de Spearman (ou coefficient de corrélation des rangs) :
C'est, dans le cas de deux variables ordinales X et Y mesurées sur les mêmes individus, le coefficient de corrélation entre le rang des individus pour X et le rang des individus pour Y.
Courbe cumulative croissante (ou fonction de répartition) :
C'est le tracé de la fonction N qui à tout x associe N ( x ) = nombre d'observations ≤ x. Il s'obtient au moyen des effectifs cumulés croissants.
Dans le cas discret on a une fonction en escalier, dans le cas continu une fonction continue, affine par morceaux.
Si on raisonne en fréquences (au lieu d'effectifs), on a le tracé de la fonction de répartition.
F ( x ) = proportion d'observations ≤ x
| Exemples : | 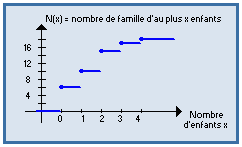
|
Courbe cumulative décroissante :
C'est le tracé de la fonction N' qui à tout x associe N' ( x ) = nombre d'observations > x. Il s'obtient au moyen des effectifs cumulés décroissants.
| Exemples : | 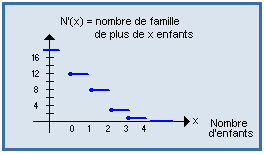
|
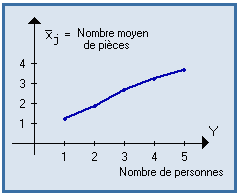
Si X et Y sont 2 variables quantitatives, la courbe de régression de Y en X est la courbe représentant les moyennes conditionnelles de Y, à X fixé.
La courbe de régression de X en Y représente les moyennes conditionnelles de X, à Y fixé.
Exemples :
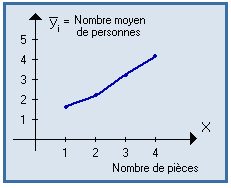 |
 |
On appelle covariance de deux variables statistiques X et Y sur les mêmes n individus le nombre :
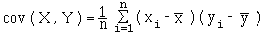 =
= 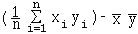
"Moyenne des produits moins le produit des moyennes"
Ce nombre est positif si X et Y ont tendance à varier dans le même sens, et négatif si elles ont tendance à varier en sens contraire.
Si les données sont groupées en ( xi , yi ) d'effectifs ni ,
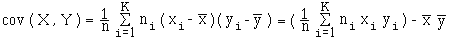
Les déciles D1 , D2 , ... , D9 divisent une série statistique en 10 parties d'effectifs égaux.
Ce sont les abscisses respectives des points d'ordonnée 0.1 ; 0.2 ; ... ; 0.9 sur la courbe cumulative croissante.
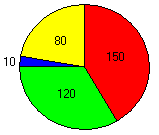
Diagramme circulaire (ou à secteurs circulaires, ou en camembert) :
Diagramme permettant de représenter la distribution d'une variable qualitative : les modalités sont représentées par des portions de disque proportionnelles à leur effectif, ou à leur fréquence.
|
Exemple : |
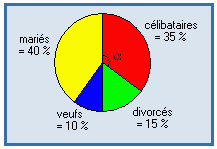 |
l'angle α est proportionnel à α = 0.15 × 360 = 54° |
Diagramme en barres (ou en tuyaux d'orgue) :
Diagramme représentant la distribution d'une variable qualitative : les modalités sont placées en abscisse, formant des bases de rectangles égales et équidistantes, et les effectifs (ou fréquences) en ordonnée, suivant une échelle arithmétique.
Les surfaces des rectangles obtenus sont proprotionnelles aux effectifs (ou aux fréquences).
|
Exemple : |
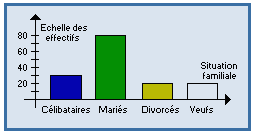 |
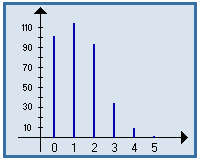
Diagramme représentant la distribution d'une variable quantitative discrète : les valeurs sont placées en abscisse, les effectifs (ou fréquences) en ordonnée, au moyen de segments verticaux.
|
Exemple : |
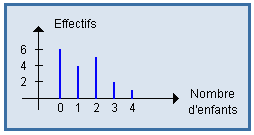 |
Diagramme en boîte (ou boîte à moustaches) :
Il s'agit d'un diagramme permettant de positionner les quartiles Q1 , Q2 , Q3 , au moyen de rectangles de largeur arbitraire, prolongés par des "moustaches" de part et d'autre, de longueur au plus égale à une fois et demie Q3 - Q1

Si la plus petite ou la plus grande valeur observée se trouvent à l'intérieur, on raccourcit les moustaches correspondantes ; si elles se trouvent à l'extérieur, on positionne à part les valeurs "aberrantes" qui dépassent des moustaches :

Ces diagrammes sont surtout utiles pour comparer rapidement l'allure générale de plusieurs distributions.
Diagramme permettant simultanément de dépouiller les données d'une série statistique et de faire une représentation graphique.
Chaque observation individuelle est représentée par sa tige (premiers chiffres, communs à plusieurs valeurs observées),et sa feuille (derniers chiffres).
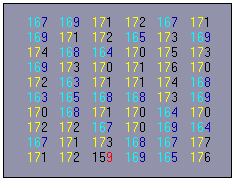 |
 |
Un paramètre statistique est dit de dispersion s'il s'agit d'un nombre clé résumant la plus ou moins grande disparité des observations, leur plus ou moins grande variabilité de part et d'autre de la tendance centrale : étendue, écart-type sont des paramètres de dispersion.
Ensemble des valeurs, modalités ou classes d'une variable statistique, et des effectifs ou fréquences associées :
Par exemple :
pour une variable qualitative : |
|
pour une variable continue : |
|
La distribution conditionnelle d'une variable Y, pour X fixé, ( X égal à xi , modalité ou valeur, ou X appartenant à une classe donnée) est la distribution statistique des valeurs de Y, en se limitant aux individus pour lesquels X est égal à xi (ou appartient à une classe donnée).
Exemple : 1) Distributions conditionnelles de l'âge, pour la catégorie X fixée :
| Catégorie | Age (années) |
| A | 32 ; 35 ; 40 ; 42 ; 43 ; 43 ; 49 ; 50 ; 55 ; 58 |
| B | 22 ; 26 ; 27 ; 27 ; 29 ; 30 ; 31 ; 31 ; 33 ; 34 ; 36 ; 36 ; 38 ; 39 ; 39 ; 42 ; 44 ; 46 ; 51 ; 53 |
| C | 20 ; 20 ; 21 ; 22 ; 23 ; 24 ; 24 ; 24 ; 26 ; 27 ; 28 ; 28 ; 28 ; 29 ; 29 ; 30 ; 32 ; 33 ; 33 ; 35 ; 38 ; 41 ; 43 ; 45 ; 45 |
Exemple : 2) Distributions conditionnelles de la catégorie, par tranche d'âge :
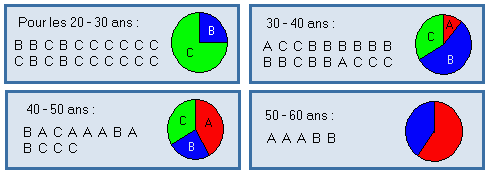
Distribution d'une variable statistique, obtenue dans la marge d'un tableau de contingence, en ajoutant les effectifs ligne par ligne, ou colonne par colonne.
Données brutes (Données statistiques brutes) :
Ensemble de mesures ou d'observations concernant l'état ou l'évolution d'un phénomène. Ce sont les valeurs prises par une ou plusieurs variables sur un certain nombre d'individus.
Séries de mesures, d'observations, d'une ou plusieurs variables statistiques sur un ensemble d'individus.
C'est la différence entre le 3ème et le 1er quartile, amplitude de l'intervalle interquartile :
C'est la racine carrée de la variance :
 pour des données groupées.
pour des données groupées.
Une distribution aura un écart-type d'autant plus faible (proche de 0) qu'elle sera ramassée autour de la moyenne, avec des valeurs très peu différentes les unes des autres.
Nombre d'individus pour lesquels une variable statistique a pris une valeur donnée. Si, sur 150 familles, 50 ont 2 enfants, on dira que l'effectif ni correspondant à la valeur xi = 2 de la variable "nombre d'enfants", est 50.
Résultat de l'addition, de proche en proche, des effectifs d'une distribution observée, soit en commençant par le 1er :
N1 = n1 , N2 = n1 + n2 , ... , Ni = n1 + n2 + ... + ni
(effectifs cumulés croissants),
soit en commençant par le dernier :
N'K = nK , N'K-1 = nK + nK-1 , ... , Ni' = nK + nK-1 + ... + ni
(effectifs cumulés décroissants).
| Exemples : |
|
C'est le nombre d'observations, d'une série statistique brute, nombre d'individus de la population étudiée.
Il est égal à la somme des effectifs associés aux différentes modalités, valeurs ou classes :
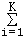 ni
niDifférence entre la plus grande et la plus petite des observations d'une série statistique. C'est un paramètre de dispersion.
C'est le tracé de la fonction N qui à tout x associe N ( x ) = nombre d'observations ≤ x. Il s'obtient au moyen des effectifs cumulés croissants.
Dans le cas discret on a une fonction en escalier, dans le cas continu une fonction continue, affine par morceaux.
Si on raisonne en fréquences (au lieu d'effectifs), on a le tracé de la fonction de répartition.
F ( x ) = proportion d'observations ≤ x
On appelle fractiles des valeurs F1 , F2 , ... , Fk-1 divisant une série en k parties d'effectifs égaux.
On a autant de valeurs ≤ F1 que de valeurs comprises entre F1 et F2 , ou entre F2 et F3 , etc.
Pour k = 4, ce sont les 3 quartiles Q1 , Q2 , Q3 (Q2 étant la médiane).
Fréquence (ou fréquence relative) :
C'est la proportion (ou le pourcentage) d'individus pour lesquels une variable statistique a pris une valeur donnée. Si, sur 150 familles, 50 ont 2 enfants, on dira que la fréquence fi correspondant à la valeur xi = 2 de la variable "nombre d'enfants", est :
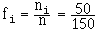 = 0.33 soit 1/3 ou 33.33 %
= 0.33 soit 1/3 ou 33.33 %
Résultat de l'addition, de proche en proche, des fréquences d'une distribution observée, soit en commençant par le 1er :
F1 = f1 , F2 = f1 + f2 , ... , Fi = f1 + f2 + ... + fi
(fréquences cumulées croissantes),
soit en commençant par le dernier :
F'K = fK , F'K-1 = fK + fK-1 , ... , F'i = fK + fK-1 + ... + fi
(fréquences cumulées décroissantes).
| Exemples : |
|
Graphique permettant de représenter une distribution continue regroupée en classes : rectangles juxtaposés dont les bases sont les classes, et les surfaces sont proportionnelles aux effectifs (ou fréquences) associés.
Si les classes sont de même amplitude ai , on place en ordonnée les effectifs ni
(ou les fréquences fi ).
Si les amplitudes ai
sont différentes, on place ni / ai
(ou fi / ai ).
|
Exemples : |
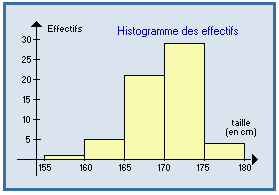
|
2 variables statistiques X et Y sont dites indépendantes si la distribution conditionnelle de Y , pour tout x , est constante (c'est-à-dire ne dépend pas de x). Cela signifie que les lignes du tableau de contingence sont proportionnelles, ou de façon équivalente que les colonnes du tableau de contingence sont proportionnelles, et donc que la distribution conditionnelle de X , pour tout y , est constante.
|
Exemples : |
|
"sexe" et "situation matrimoniale" sont ici deux variables indépendantes.
Individu (ou unités statistiques) :
Les individus sont les éléments de la population statistique étudiée. Pour chaque individu, on dispose d'une ou plusieurs observations.
| Exemples : |
|
Inégalité de (Bienaymé)-Tchébichev :
Pour toute population de moyenne 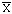 et d'écart-type s ,
la proportion de valeurs de l'intervalle [
et d'écart-type s ,
la proportion de valeurs de l'intervalle [ 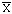 - k s ;
- k s ; 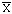 + k s ] est
d'au moins égale à 1 -
+ k s ] est
d'au moins égale à 1 - 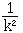 , pour tout k ³ 1.
, pour tout k ³ 1.
Par exemple, 75 % des valeurs au moins appartiennent à :
[ 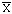 - 2 s ;
- 2 s ; 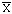 + 2 s ], c'est-à-dire s'écartent de moins de 2 écart-types de la moyenne.
+ 2 s ], c'est-à-dire s'écartent de moins de 2 écart-types de la moyenne.
C'est l'intervalle entre le 1er et le 3ème quartile : [ Q1 Q3 ].
Il contient 50 % des observations ; 25 % sont inférieures et 25 % sont supérieures.
C'est l'intervalle du milieu d'une série statistique comprenant un nombre pair d'observations :

La médiane M d'une série statistique rangée par ordre croissant
x(1) < x(2) < .... < x(n) est la valeur "du milieu", soit x(p+1) si n est impair et vaut 2 p + 1, ou
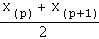 si n est pair et vaut 2 p
si n est pair et vaut 2 p
M est l'abscisse du point d'intersection des courbes cumulatives, d'ordonnée n/2 en effectifs ou 0.5 en fréquences.
Les modalités d'une variable qualitative sont les différentes valeurs que peut prendre celle-ci.
Par exemple les modalités de la variable "situation familiale" sont : célibataire, marié, veuf, divorcé.
Les modalités de la variable "sexe" sont : féminin, masculin (pouvant être codées par exemple 0 et 1).
C'est le quotient 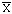 de la somme d'une série d'observations par leur nombre.
de la somme d'une série d'observations par leur nombre.
Pour une série brute x1 , x2
, .... , xn , 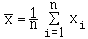
Pour une série groupée ( xi , ni ) ,
i = 1, ... , K , 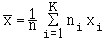
Les moyennes conditionnelles sont les moyennes des distributions conditionnelles : valeurs moyennes de Y , pour X fixé ou valeurs moyennes de X , pour Y fixé.
La moyenne des nombres x1 , x2 , ... , xn , pondérée par les poids p1 , p2 , ... , pn (nombres positifs de somme 1) est égale à :
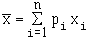
Dans le calcul de cette moyenne, les valeurs ayant un poids important comptent davantage que celles ayant un poids faible.
Ensemble de points isolés représentés dans un graphique cartésien : points M1
, M2 , ... , Mn
de coordonnées ( x1 , y1
) ; ( x2 , y2 ) ; ... ;
( xn , yn ).
|
Exemples : taille et poids de 60 enfants |
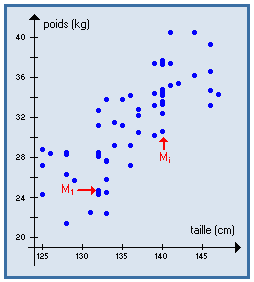 |
Ce sont quelques nombres permettant de résumer numériquement les traits principaux d'une distribution statistique.
Par exemple : la moyenne, l'écart-type, l'étendue sont des paramètres statistiques.
Une population statistique est l'ensemble sur lequel on effectue des observations.
| Exemples : |
|
Un paramètre statistique est dit de position s'il s'agit d'un nombre clé permettant de préciser où se répartit une certaine fraction des observations ainsi les quartiles permettent de situer le 1/4 inférieur, la moitié, le 1/4 supérieur des observations.
Ce sont les distributions conditionnelles, écrites en fréquences et non en effectifs.
On peut les représenter graphiquement par :
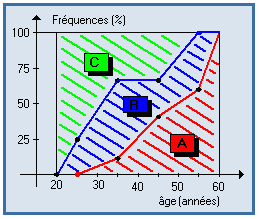
Les quartiles Q1 , Q2 , Q3 divisent une série statistique en 4 parties d'effectifs égaux : 25 % des valeurs sont ≤ Q1 , 25 % comprises entre Q1 et Q2 ; 25 % entre Q2 et Q3 , et 25 % supérieures à Q3.
Q1 , Q2 , Q3 sont respectivement l'abscisse des points d'ordonnées 0.25 ; 0.5 ; 0.75 sur la courbe cumulative croissante. Q2 est égal à la médiane.
Si X est une variable ordinale mesurée sur n individus, le rang de l'individu i pour X est le numéro d'ordre de i, si on range toutes les valeurs xi par ordre croissant.
Exemple : si les xi obtenus sont : O R D R E ; le rang de l'individu n° 3, pour l'ordre alphabétique, est 1 ; le rang de l'individu n° 5 est 2, etc ...
C'est
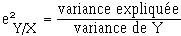
coefficient compris entre 0 et 1 mesurant la part plus ou moins grande de la variabilité d'une variable Y qui peut être expliquée par les variations d'une autre variable X, qualitative, discrète, ou continue découpée en classes.
Série statistique (ou distribution observée) :
Ensemble des modalités, valeurs, ou classes d'une variable, avec les effectifs observés correspondants.
|
Exemples : |
|
Statistique descriptive univariée :
La Statistique descriptive univariée consiste en la description de chacun des caractères statistiques, un par un, et non des liens éventuels existant entre eux.
Statistique descriptive bivariée :
La Statistique descriptive bivariée consiste en la description de deux variables mesurées simultanément sur les mêmes individus. Elle permet de mettre en évidence le type de lien existant éventuellement entre ces variables.
Partie de la statistique qui, contrairement à la statistique descriptive, ne se contente pas de décrire des observations, mais extrapole les constatations faites à un ensemble plus vaste, permet de tester des hypothèses sur cet ensemble, et de prendre des décisions le concernant. [Voir les modules "Echantillonnage-Estimation" et "Tests"]
Tableau résultant du tri croisé de deux variables.
| Y | ||||||||||||||||
| X |
|
Un paramètre statistique est dit de tendance centrale s'il s'agit d'un nombre clé autour duquel les observations sont réparties : mode, médiane, moyenne sont des paramètres de tendance centrale.
Tri à plat d'une série statistique brute :
C'est l'inventaire des modalités ou valeurs rencontrées dans la série, avec les effectifs correspondants.
|
 |
||||
|
 |
A partir de 2 variables X et Y mesurées sur les mêmes individus, décompte des effectifs correspondant à chaque couple ( xi , yj ) :
nombre d'individus pour lesquels X = xi et Y = yj
Une distribution est unimodale si elle présente un maximum marqué, correspondant à une valeur appelée mode.
S'il y a plusieurs maxima relatifs, la distribution est plurimodale (bimodale dans le cas 2)
Unité statistique (ou individu(s) ) :
Les individus sont les éléments de la population statistique étudiée.
Pour chaque individu, on dispose d'une ou plusieurs observations.
| Exemples : |
|
C'est une variable quantitative pouvant prendre par nature une infinité de valeurs, généralement tout un intervalle réel.
| Exemples : |
|
C'est une variable qualitative qui ne peut prendre que 2 modalités : OUI ou NON ; masculin ou féminin ; bon ou mauvais , etc....
C'est une variable quantitative pouvant prendre par nature un nombre fini (ou dénombrable) de valeurs.
| Exemples : |
|
Variable qualitative (ou caractère qualitatif) :
Une variable statistique est qualitative si ses valeurs, ou modalités, s'expriment de façon littérale ou par un codage sur lequel les opérations arithmétiques telles que moyenne, somme, ... , n'ont pas de sens.
| Exemples : |
|
Variable qualitative nominale :
C'est une variable qualitative dont les modalités ne sont pas ordonnées.
| Exemples : |
|
Variable qualitative ordinale :
C'est une variable qualitative dont les modalités sont naturellement ordonnées selon un ordre total : on peut dire que selon un certain sens la modalité A est moins forte que la B, qui est moins forte que la C, etc...
| Exemples : |
|
Variable quantitative (ou caractère quantitatif) :
Une variable statistique est quantitative si ses valeurs sont des nombres sur lesquels des opérations arithmétiques telles que somme, moyenne, ... ont un sens.
| Exemples : |
|
Variable statistique (ou caractère statistique) :
C'est ce qui est observé ou mesuré sur les individus d'une population statistique. Il peut s'agir d'une variable qualitative ou quantitative.
| Exemples : |
|
C'est la moyenne des carrés des écarts à la moyenne :
s² = 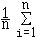 ( xi
-
( xi
- 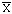 )² pour des données isolées, et
)² pour des données isolées, et
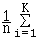 ( ni)( xi
-
( ni)( xi
- 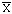 )² pour des données groupées.
)² pour des données groupées.
( xi est le centre de classe dans le cas de données regroupées en classes).
On peut aussi calculer la variance par :
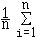 ( x²i ) -
( x²i ) - 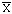 ²
ou
²
ou 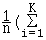 ni
x²i) -
ni
x²i) - 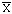 ²
²
Par exemple : la variance de la série : 8 9 10 10 12 14 14 16, qui a pour moyenne 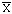 = 11.625 est :
= 11.625 est :
s² =  [ (8 - 11.625)² + (9 - 11.625)² + 2 (10 - 11.625)² + (12 - 11.625)² + 2 (14 - 11.625)² + (16 - 11.625)² ]
[ (8 - 11.625)² + (9 - 11.625)² + 2 (10 - 11.625)² + (12 - 11.625)² + 2 (14 - 11.625)² + (16 - 11.625)² ]
=  (8² + 9² + 2 × 10² + 12² + 2 × 14² + 16²) - (11.625)² = 6.9844
(8² + 9² + 2 × 10² + 12² + 2 × 14² + 16²) - (11.625)² = 6.9844
La racine carrée de la variance est l'écart-type, qui s'exprime dans la même unité que les xi et mesure la plus ou moins grande dispersion des valeurs de part et d'autre de la moyenne.
C'est la variance des moyennes des distributions conditionnelles : si Y est quantitative, et si X subdivise
l'ensemble des individus en K classes d'effectifs n1 ,
n2 , ... , nK
telles que la moyenne de Y sur chaque classe est : 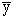 1 , ... ,
1 , ... ,
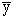 K ,
K ,
la variance de Y expliquée par X est :
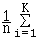 ( ni
( ni
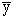 ²i ) -
²i ) - 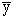 ²
²
C'est la moyenne des variances des distributions conditionnelles, pondérées par les effectifs. SiY est quantitative, et si X subdivise l'ensemble des individus en K classes d'effectifs n1 , n2 , ... , nK telles que la moyenne de Y sur chaque classe est :
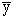 1 , ... ,
1 , ... , 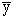 K ,
K ,
avec les variances s²1 , s²2 , ..., s²K , la variance de Y se décompose en :
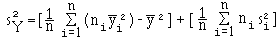
Le premier terme de la somme est la variance de Y expliquée par X, le second la variance résiduelle.