Somme des carrés des résidus d'un modèle

Calculons :

a = et b

On a :

Cov ( X , Y ) = 3.81

s² ( X ) = 0.04

et a = = 94.79

= a + b

b = - a = 58.58 - ( 94.79 * 0.354 ) = 25

Le modèle obtenu par la méthode des moindres carrés est : Y = 94.79 X + 25

Ce modèle est celui qui rend minimum la somme des carrés des résidus ( SCR ).

Observation X Y R = y - R² = ( y - )²
1
2
3
4
5
6
7
8
9
10
11
12		 0.10
0.30
0.15
0.60
0.70
0.20
0.30
0.15
0.55
0.60
0.20
0.40		 35.80
52.20
40.00
84.90
88.50
43.40
56.80
38.70
78.30
82.20
41.10
61.00		 34.48
53.44
39.22
81.88
91.36
43.96
53.44
39.22
77.14
81.88
43.96
62.92		 1.32
-1.24
0.78
3.02
-2.86
-0.56
3.36
-0.52
1.16
0.32
-2.86
-1.92		 1.74
1.54
0.61
9.14
8.16
0.32
11.28
0.27
1.35
0.10
8.19
3.68
Somme 4.25 702.9     46.38
Moyenne 0.35 58.58      

 

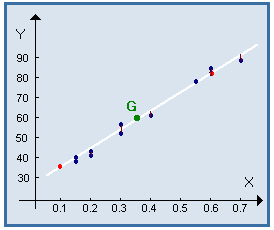
Avec le modèle obtenu par la méthode des moindres carrés, la somme des carrés des résidus est :

SCR = 46.38

Elle est bien inférieure à la somme des carrés des résidus, obtenue en choisissant empiriquement comme modèle, l'équation de la droite passant par les points 1 et 10.

Dans ce cas on avait : SCR = 56.19

 

Développement