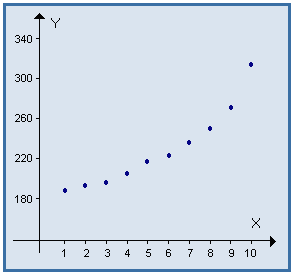
Evolution du coût de la construction : essai d'ajustement à un modèle exponentiel

Considérons des observations ( x_i , y_i ) relatives à deux variables X et Y, et le nuage de points correspondant :

Par exemple, l'évolution de l'indice du coût de la construction selon l'INSEE (base 100 en 1953)

Observation X Y 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 1 2 3 4 5 6 7 8 9 10 188 193 196 205 217 223 236 250 271 314

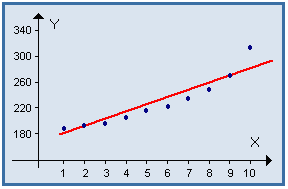Essayons d'expliquer la variation de l'indice Y , en fonction du rang X de l'année par un modèle affine :

Y = f ( x ) = a X + b

en ajustant une droite à ce nuage de points par la méthode des moindres carrés.

On obtient l'équation de la droite d'ajustement de Y en X : Y = 12.418 X + 161

Calculons les valeurs théoriques prévues par le modèle, et les résidus :

X Y ei = Y - 1 2 3 4 5 6 7 8 9 10 188 193 196 205 217 223 236 250 271 314 173.42 185.84 198.25 210.67 223.09 235.51 247.93 260.35 272.76 285.19 14.58 7.16 -2.25 -5.67 -6.09 -12.51 -11.93 -10.35 -1.76 28.82

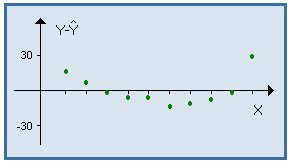Le nuage des résidus a une forme curviligne qui indique que le modèle affine n'est pas adéquat pour représenter le phénomène.

On procède alors par changement de variable.

On pose : V = log Y

Si on procède à un ajustement affine de V en X : log Y = V = c X + d

Alors : Y = k a^X avec k = 10^d et a = 10^c

et on obtient Y comme fonction exponentielle de X .

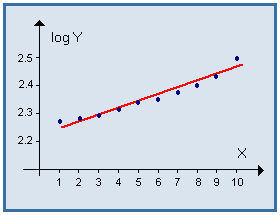
Les points du nuage semblent assez bien alignés.

La droite d'ajustement de V en X a pour équation : V = 0.0228 X + 2.2296

X Y V = log Y V - 1 2 3 4 5 6 7 8 9 10 188 193 196 205 217 223 236 250 271 314 2.2742 2.2856 2.2923 2.3117 2.3365 2.3483 2.3729 2.3979 2.4330 2.4969 2.2524 2.2751 2.2979 2.3207 2.3435 2.3663 2.3891 2.4120 2.4347 2.4575 0.0218 0.0104 -0.0057 -0.0089 -0.0071 -0.0180 -0.0162 -0.0140 -0.0017 -0.0394

Calculons les valeurs théoriques, les résidus associés, et représentons le nuage des résidus :

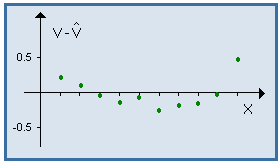
De : V = log Y = 0.0228 X + 2.2296

on tire : Y = ( 169.657 ) * ( 1.054 )^X

On prendra cette relation comme modèle du phénomène considéré.

X	Y		Y -
1 2 3 4 5 6 7 8 9 10	188 193 196 205 217 223 236 250 271 314	178.80 188.43 198.58 209.28 220.56 232.44 244.97 258.17 272.08 286.74	9.20 4.57 -2.58 -4.28 -3.56 -9.44 -8.97 -8.17 -1.08 27.26