LEXIQUE :
Choisissez le terme à expliquer...Soit E une expérience aléatoire n'ayant qu'un nombre fini d'issues.
Soit Ω l'ensemble de ces issues. ( P( Ω ) , ∪ , ∩ , - ), c'est-à-dire l'ensemble P ( Ω )
des parties de Ω muni des opérations d'union, d'intersection, de complémentation, s'appelle l'algèbre des événements à l'expérience aléatoire
E.
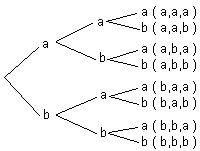
Arborescence : (ou diagramme en arbre)
A l'aide d'une arborescence on peut construire les éléments de X3
où X = { a , b }
Soit n un entier naturel, X un ensemble.
Une n-liste sans répétition d'éléments de X s'appelle aussi un arrangement de n éléments pris parmi les éléments de X.
Soit X un ensemble à m éléments
et n un entier naturel tel que 0 ≤ n ≤ m.
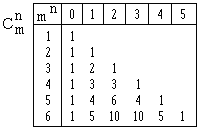
X a 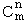 parties à n éléments, avec :
parties à n éléments, avec :

Une partie à n éléments d'un ensemble à m éléments s'appelle aussi une combinaison de n éléments de X.
Les nombres 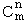 s'appellent les coefficients binômiaux.
s'appellent les coefficients binômiaux.
Exemple : Une entreprise compte 8 ingénieurs compétents pour diriger certains travaux. Mais 3 ingénieurs suffisent pour mener à bien la tâche en question. Il y a :
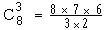 = 56 façons de désigner les 3 ingénieurs.
= 56 façons de désigner les 3 ingénieurs. On a : 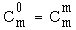 = 1
= 1
Un ensemble X à m éléments a une partie à 0 élément et une seule, la partie vide, et une seule partie à m éléments : lui-même.
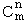 = Cm
= CmDans un ensemble à m éléments, il y a autant de parties à n éléments
( 0 ≤ n ≤ m ) que de parties à m-n éléments.
Si y a n éléments,  le complémentaire dans X de Y à m-n éléments. On a la relation :
le complémentaire dans X de Y à m-n éléments. On a la relation :
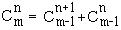 (Formule de Pascal)
(Formule de Pascal)qui permet de calculer de proche en proche les coefficients binômiaux.
Une partie à n éléments d'un ensemble à m éléments s'appelle aussi une combinaison de n éléments de X.
Soit A une partie d'un ensemble X,
on appelle complémentaire de A, la partie notée 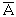 où X / A de X formée des x ∈ X
tels que x ∉ A.
où X / A de X formée des x ∈ X
tels que x ∉ A.
Si :
X = { 1, 2, 3, 4, 5, 6 } ,
A = { 1, 2 } ,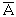 = { 3, 4, 5, 6 }
= { 3, 4, 5, 6 }
Conjonction de deux événements :
Soit E une expérience aléatoire, A et B deux événements liés à cette expérience. On appelle conjonction de ces événements, l'événement "A et B".
"A et B" est réalisé si A et B sont réalisés. "A et B" n'est pas réalisé si l'un des événements A ou B n'est pas réalisé.
Exemple : Soit E l'expérience aléatoire qui consiste à lancer un dé, et dont les issues sont les nombres qui apparaissent sur la face supérieure du dé, après immobilisation.
Soit A l'événement "le numéro est pair" et B l'événement "le numéro est un multiple de 3". A et B est l'événement "le numéro est un 6".
Les couleurs d'une carte sont traditionnellement : trèfle, carreau, coeur, pique.
Disjonction de deux événements :
Soit E une expérience aléatoire, A et B deux événements liés à cette expérience. On appelle disjonction de ces événements, l'événement "A ou B".
"A ou B" est réalisé si l'un des deux événements A ou B est réalisé. "A ou B" n'est pas réalisé si aucun des deux événements A ou B n'est réalisé.
Exemple : Soit E l'expérience aléatoire qui consiste à lancer un dé, et dont les issues sont les nombres qui apparaissent sur la face supérieure du dé, après immobilisation.
Soit A l'événement "le numéro est pair" et B l'événement "le numéro est un multiple de 3". A ou B est l'événement "le numéro est l'un des nombres : 2, 3, 4, 6".
Echantillon ordonné avec remise :
Une urne contient m objets, numérotés de 1 à n.
On prélève un premier objet de l'urne, on note son numéro et on le replace dans l'urne. On prélève un deuxième objet de l'urne, on note son numéro et on le replace dans l'urne. On répète cette opération n fois. On dit qu'on a prélevé un échantillon de n objets avec remise.
Il y a mn tels échantillons.
Echantillon ordonné sans remise :
Soit X un ensemble à m éléments. Un échantillon ordonné sans remise d'éléments de X est obtenu de la manière suivante :
- on prélève un premier élément de X, et on ne le replace pas dans X.
- on prélève un deuxième élément de X, et on ne le replace pas dans X
On poursuit ainsi jusqu'à l'obtention du nième élément. Il y a :
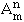 = m (m-1) ... (m - n + 1)
= m (m-1) ... (m - n + 1)échantillons ordonnés sans remise d'éléments de X, si X a m éléments.
Exemple : Un juge d'instruction ne peut recevoir que quatre personnes par jour. Il dispose de 20 témoins dans une affaire. Il doit donc convoquer 4 de ces témoins pour une de ses journées de travail. Il les recevra les unes après les autres.
Il s'agit d'un échantillon ordonné et sans remise de 4 témoins parmi les 20.
Il y a 20 × 19 × 18 × 17 = 116 280 manières d'organiser les rendez-vous de cette journée.
Echantillon non ordonné avec remise :
Considérons une urne contenant quatre boules de couleurs différentes. On tire une boule de l'urne, on note sa couleur et on la replace dans l'urne. On répète l'opération cinq fois.
Soit x1 ( resp. x2,
x3, x4,
x5 ) le nombre de boules obtenues de la 1ère couleur
(resp. 2e, 3e, 4e, 5e).
On ne s'intéresse pas à l'ordre dans lequel sont sorties les couleurs, mais seulement au nombre de boules de chaque couleur.
On dit qu'on a extrait de l'urne un échantillon non ordonné avec remise de 4 boules.
On a x1
+ x2 + x3
+ x4 + x5 = 5.
Il y a donc : 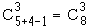 tels échantillons.
tels échantillons.
On prélève dans une urne contenant n boules de couleurs différentes une boule. On note la couleur de la boule. On la replace dans l'urne et on répète cette opération m fois. On note le nombre de boules de chaque couleur que l'on a obtenue. On dit que l'on a extrait de l'urne un échantillon non ordonné avec remise de m boules.
D'une manière générale si l'urne contient n boules de couleurs différentes, il y a :
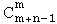 combinaisons non ordonnées avec remises des n boules.
combinaisons non ordonnées avec remises des n boules.
Echantillon ordonné sans remise :
Définition : Prélever simultanément n objets parmi m c'est prélever un échantillon de n objets non ordonné sans remise parmi m.
Il y a 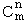 façons de prélever un échantillon non ordonné sans remise parmi n objets.
façons de prélever un échantillon non ordonné sans remise parmi n objets.
Exemple : Pour connaître l'opinion de ses employés une entreprise décide d'interroger 40 d'entre eux. Sachant qu'il y a 1000 employés dans
l'entreprise, il y a donc 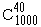 façons de désigner les 40 employés qui seront interrogés :
façons de désigner les 40 employés qui seront interrogés :
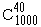 = 5 559 744 236 × 1071
= 5 559 744 236 × 1071
Soit X un ensemble, on note P ( X ) l'ensemble dont les éléments sont les parties de X.
P ( X ) s'appelle l'ensemble des parties de X.
Exemple : Si X = { a, b, c } , P ( X ) a 8 éléments.
- l'ensemble vide : ∅
- la partie à un élément : { a } , { b } , { c }
- la partie à deux éléments : { b, c } , { a , c } , { a, b }
- la partie à trois éléments : { a, b, c }
On appelle épreuve d'une expérience aléatoire chaque répétition de cette expérience.
Soit E une expérience aléatoire ayant un nombre fini d'issues.
Soit Ω = { w1, w2 , ... , wn } l'ensemble de ces issues.
On dit que l'on fait l'hypothèse d'équiprobabilité lorsque pour la probabilité P définie sur P ( Ω ), tous les événements élémentaires { wi } ont la même probabilité. Alors
P( { wi }) = 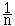 où n = card( Ω )
où n = card( Ω )
Exemple : Soit E l'expérience aléatoire consistant à jeter un dé. Cette expérience à 6 issues. Ω = { 1, 2, 3, 4, 5, 6 }.
Soit P : P( Ω ) → [0, 1] une probabilité définie sur P ( Ω ). On a fait l'hypothèse d'équiprobabilité si
P({ 1 }) = P({ 2 }) = P({ 3 }) = P({ 4 }) = P({ 5 }) = P({ 6 }) = 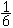
Chaque face du dé a la même probabilité d'apparition.
Soit E une expérience aléatoire ayant un nombre fini d'issues.
Soit Ω l'ensemble des issues.
P : P ( Ω ) → [0, 1] une probabilité.
Le triplet ( Ω , P ( Ω ) , P ) s'appelle un espace probabilisé.
Etant donné une expérience aléatoire, on appelle événement lié à cette expérience aléatoire, toute assertion, qui peut être vraie ou fausse suivant l'issue de l'expérience.
Exemple : Si on considère l'expérience aléatoire qui consiste à jeter un dé, cette expérience a six issues : 1, 2, 3, 4, 5, 6 correspondant au numéro qui apparaît sur la face supérieure du dé lorsqu'il s'est immobilisé sur la table.
L'assertion "le numéro sur la face supérieure est pair" est un événement lié à cette expérience aléatoire.
Soit E une expérience aléatoire et A un événement lié à cette expérience aléatoire. On dit que A est un événement certain, s'il est réalisé quelle que soit l'issue de l'expérience E.
Exemple : Soit E l'expérience aléatoire qui consiste à jeter un dé et dont les issues sont les numéros qui apparaissent sur la face supérieure du dé après immobilisation.
L'événement "le numéro sur la face supérieure du dé est inférieur à 7" est un événement certain.
Soit E une expérience aléatoire, un événement A lié à l'expérience E, est dit un événement élémentaire s'il n'est réalisé que par une seule issue de cette expérience.
Exemple : Soit l'expérience aléatoire qui consiste à jeter un dé, et dont les issues sont l'un des 6 numéros figurant sur la face supérieure après immobilisation du dé.
L'événement "le numéro sur la face supérieure du dé est le 4" est un événement élémentaire. Il y a autant d'événements élémentaires que d'issues à une expérience aléatoire.
Soit E une expérience aléatoire et A un événement lié à cette expérience aléatoire. On dit que A est un événement impossible, s'il n'est pas réalisé, quelle que soit l'issue de l'expérience E.
Exemple : Soit E l'expérience aléatoire qui consiste à jeter un dé et dont les issues sont les numéros qui apparaissent sur la face supérieure du dé après immobilisation.
L'événement "le numéro sur la face supérieure du dé est le numéro 7" est un événement impossible.
Etant donné une expérience aléatoire E et deux événements liés à cette expérience aléatoire, on dit qu'ils sont incompatibles s'ils ne peuvent pas se réaliser simultanément.
Exemple : Soit E l'expérience aléatoire consistant à lancer un dé, et dont les issues sont les numéros qui apparaissent sur la face supérieure du dé après immobilisation.
Les événements "le numéro sur la face supérieure est inférieur ou égal à 2 " et "le numéro sur la face supérieure est supérieur ou égal à 5" sont incompatibles.
Soit ( Ω , P ( Ω ), P) un espace probabilisé fini, A et B deux événements liés à cet espace. On dit que A et B sont indépendants pour la probabilité P si P(A ∩ B) = P( A ) P( B )
Propriétés :
1) Si la paire d'événements { A , B } est indépendante pour la probabilité P, il en est de même des paires d'événements { A , 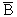 },
{
},
{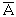 , B} , {
, B} , {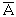 ,
, 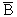 }.
}.
2) SiP(A) = 0 , A et B sont indépendants quel que soit B ∈ P ( Ω )
3) Si P(A) = 1 , A et B sont indépendants quel que soit B ∈ P ( Ω )
Exemple : Pour une entreprise de spectacle dans le département A, la probabilité de l'événement "faire l'objet d'un contrôle de sécurité" est 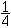 tandis que dans le département B, la probabilité n'est que de
tandis que dans le département B, la probabilité n'est que de 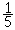 , ces deux
événements étant indépendants.
, ces deux
événements étant indépendants.
Un groupe financier possède deux entreprises de spectacle, l'une dans le département A, l'autre dans le département B. La probabilité que les deux entreprises subissent un contrôle est :
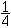 ×
× 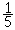 =
= 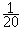
Evénements mutuellement indépendants :
Soit ( Ω , P ( Ω ) , P) un espace probabilisé et A1 , A2
, ... , An ,
n événements liés à cet espace.
On dit que ces événements sont mutuellement indépendants pour la probabilité P si tout sous-ensemble de deux ou plusieurs de ces événements satisfait à la propriété suivante : la probabilité de la conjonction des événements du sous-ensemble est le produit de leurs probabilités.
Une expérience aléatoire est une expérience dont on ne peut pas prévoir le résultat.
Exemple : Si on lance une pièce de monnaie, on ne peut pas prévoir sur quelle face elle retombera.
Lancer une pièce de monnaie est une expérience aléatoire.
Si n est un entier naturel, on appelle factorielle n, et on note n ! , le produit des n premiers entiers naturels.
1 ! = 1
2 ! = 2 × 1 = 2
3 ! = 3 × 2 × 1 = 6
4 ! = 4 × 3 × 2 × 1 = 24 etc ....
n ! est égal au nombre de permutations d'un ensemble X à n éléments.
Formule des probabilités totales :
Soit ( Ω , P ( Ω ) , P) un espace probabilisé fini. B1 , B2 , ... , Bn un système complet d'événements A ∈ P ( Ω ). On a :
P(A) = P(A | B1 ) P( B1 ) + P(A | B2 ) P( B2 ) + ... + P(A | Bn ) P( Bn )
cette formule s'appelle la formule des probabilités totales.
Exemple : Une grande marque de produits laitiers a trois usines où sont fabriqués les yaourts qu'elle commercialise à Arras, Brest et Caen.
Arras fournit 25 % de la production, Brest 20 % et Caen 55 %. On considère un yaourt de cette marque. Soit A (resp. B , C ) l'événement "le yaourt est produit par Arras (resp. Brest, Caen)".
P( A ) = 0.25
P( B ) = 0.2
P( C ) = 0.55
A, B, C constitue un système complet d'événements.
20 % des yaourts produits à Arras sont aux fruits ainsi que 30 % de ceux produits à Brest, 15 % de ceux produits à Caen.
Soit Y l'événement "le yaourt est aux fruits"
P(Y | A) = 0.2
P(Y | B) = 0.3
P(Y | C) = 0.15
D'où P( Y ) = 0.25 × 0.2 + 0.2 × 0.3 + 0.55 × 0.15
= 0.05 + 0.06 + 0.0825
= 0.1925
Soit ( Ω , P ( Ω ) , P) un espace probabilisé fini. A , B des événements,
P( A ) ≠ 0 , P( B ) ≠ 0.
On a P(B | A) = 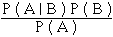 (Première formule de Bayes)
(Première formule de Bayes)
Soit B1 , B2 , ... , Bn un système complet d'événements
A, un événement ; pour i ∈ [[ 1, n ]]
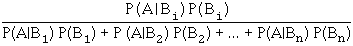
Exemple : Une grande marque de produits laitiers fabrique les yaourts qu'elle commercialise dans trois usines, implantées à Arras, Brest et Caen.
Arras fournit 25 % de la production, Brest 20 % et Caen 55 %. On achète un yaourt de cette marque.
Soit A (resp. B , C ) l'événement "le yaourt est produit par Arras (resp. Brest, Caen)"
P( A ) = 0.25
P( B ) = 0.2
P( C ) = 0.55
A, B, C constituent un système complet d'événements.
20 % des yaourts produits à Arras sont aux fruits ainsi que 30 % des yaourts produits à Brest et 15 % de ceux produits à Caen.
Soit Y l'événement "le yaourt est aux fruits"
P(Y | A) = 0.2
P(Y | B) = 0.3
P(Y | C) = 0.15
D'où P( Y ) = 0.25 × 0.2 + 0.2 × 0.3 + 0.55 × 0.15
= 0.05 + 0.06 + 0.0825
= 0.1925
Sachant que le yaourt est aux fruits, quelle est la probabilité qu'il ait été fabriqué à Caen :
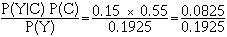 = 0.42857
= 0.42857
Formule du crible : (Formule du crible ou de Poincaré)
Si X , Y , Z sont trois ensembles.
card(X ∪ Y ∪ Z) = card( X ) + card( Y ) + card( Z ) - card(Y ∩ Z)
On généralise cette formule à n ensembles X1, X2 , ... , Xn
Si A = 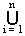 Xi
Xi
card( A ) = 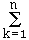 (- 1)p+1
(- 1)p+1
![]() card(
card( 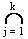 Aij )
Aij )
Dans un jeu de 32 cartes, il y a 7 hauteurs : 7, 8, 9, 10, valet, dame, roi, as.
Dans un jeu de 52 cartes, il y a 13 hauteurs : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, valet, dame, roi.
Intersection de deux parties :
Soit X un ensemble. A et B deux parties de X.
On appelle intersection des deux parties A et B, la partie notée
A ∩ B de X, constituée des x
∈ X, tels que x ∈ A ou x
∈ B.
On appelle issue d'une expérience aléatoire l'un des résultats possibles de cette expérience.
Exemple : Si on lance une pièce de monnaie, cette expérience aléatoire a deux issues :
- la pièce retombe sur face.
- la pièce retombe sur pile.
Soit n ∈ N. On appelle n-liste ( x1 , x2 , ... , xn ) d'éléments d'un ensemble X toute liste d'éléments de X, donnée dans cet ordre.
Si X = { a, b, c, d } , ( a, d, c ) est une 3-liste d'éléments de X. Elle diffère de la 3-liste ( c, d, a ).
On note Xn l'ensemble des n-listes d'éléments de X.
card( Xn ) = card( X )n
Si X a n éléments, Xn a mn éléments.
Soit n un entier naturel, X un ensemble.
Une n-liste ( x1 , x2 , ... , xn ) d'éléments de X est dite sans-répétition, si pour i ∈ [[ 1, n ]] et j ∈ [[ 1, n ]] xi ≠ xj c'est-à-dire si tous les éléments xi sont distincts.
Exemple : Parmi les 100 candidats à un concours, les 20 lauréats sont classés par ordre de mérite, sans ex-aequo.
Si X est l'ensemble des candidats, la 20-liste des lauréats classés par ordre de mérite est une n-liste sans répétition.
Si X a m éléments, il y a : 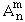 = m (m-1) ... (m - n + 1)
= m (m-1) ... (m - n + 1)
n-listes sans répétition d'éléments de X.
Soit E une expérience aléatoire, A un événement lié à cette expérience. On appelle négation de A, l'événement non A, non A est réalisé si A ne l'est pas et non A n'est pas réalisé si A l'est.
Exemple : Soit E l'expérience aléatoire qui consiste à lancer un dé, et dont les issues sont les numéros qui apparaissent sur la face supérieure du dé, après immobilisation.
Soit A l'événement "le numéro est pair", non A est l'événement "le numéro est impair".
Soit X un ensemble, on appelle partie vide de X, le complémentaire de X dans X. On la note ∅.
∅X = X - X
On démontre que ∅X = ∅Y si X et Y sont deux ensembles distincts.
On note ∅ = ∅X = ∅Y , ∅ s'appelle l'ensemble vide.
Partie d'un ensemble ou sous-ensemble :
Si X = { a , b , c , d }
Y = { a , b } est une partie de X , comme
Z = { b , c , d }
L'ensemble des parties d'un ensemble X, se note P ( X ).
Si X a n éléments , P ( X ) a zn éléments.
Soit X un ensemble. Y un autre ensemble. On dit que Y est une partie de X, si tout y de Y est aussi élément x de X. On note :
Exemple : Soit X l'ensemble des lettres de l'alphabet latin et Y l'ensemble des voyelles de l'alphabet latin. Y est une partie de X.
On dit aussi que Y est un sous-ensemble de X.
Soit X un ensemble.
A1 , A2 , ... , An n parties de X non vides, deux à deux disjointes, et dont la réunion est égale à X.
On dit que les parties A1 , A2 , ... , An constituent une partition de X.
Les parties Ai s'appellent les classes de la partition.
Exemple : Soit X la liste des communes françaises. Soit Ai
l'ensemble des communes appartenant au ième département :
A34 l'ensemble des communes de l'Hérault.
A1 , A2 , ... , A9 constitue une partition de X.
Si X est un ensemble à n éléments, une n-liste sans répétition d'éléments de X s'appelle une permutation d'éléments de X.
Si X a n éléments , il y a 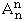 = n ( n - 1 ) ... 3.2.1 permutations des n éléments de X.
= n ( n - 1 ) ... 3.2.1 permutations des n éléments de X.
On note 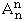 = n ! qui se lit "factorielle n".
= n ! qui se lit "factorielle n".
Exemple : 9 soldats doivent se ranger en lignes.
Il y a 9 ! façons pour eux de le faire, soit 362 880 manières de le faire.
Principe d'inclusion-exclusion :
Si X et Y sont deux ensembles
card(X ∪ Y) = card( X ) + card( Y ) - card(X ∩ Y)
Exemple : Dans une école :
120 étudiants étudient l'anglais
90 étudiants étudient l'espagnol
40 étudiants étudient à la fois l'anglais et l'espagnol.
Il y a donc : 120 + 90 - 40 = 170 étudiants qui étudient soit l'anglais, soit l'espagnol.
Soit E une expérience aléatoire ayant un nombre fini d'issues. Soit Ω l'ensemble de ces issues. On appelle probabilité, toute application :
P : P ( Ω ) → [ 0 , 1 ]
vérifiant :
1) P( Ω ) = 1
2) Si A ∩ B = ∅
P(A ∪ B) = P( A ) + P( B )
Soit ( Ω , P ( Ω ) , P) un espace probabilisé fini et A un événement lié à cet espace tel que P( A ) ≠ 0 .
On considère l'application : PA : P ( Ω ) → ![]()
définie par : P(B | A) = 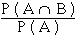
PA( B ) qui se note aussi P(A | B) s'appelle la probabilité conditionnelle de B sous la condition de réalisation de A.
On lit aussi P(A | B) = PA( B ) , probabilité de B sachant A.
On démontre que PA définit une probabilité sur P( Ω ).
En particulier P(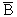 | A) = 1 - P(B | A).
Si B et C sont incompatibles :
| A) = 1 - P(B | A).
Si B et C sont incompatibles :
PA(B ∪ C) = P(B | A) + P(C | A)
On a P(A ∩ B) = P( A ) P(B | A) = P( B ) P(A | B)
Exemple : Une enquête montre que 4 % des français sont atteints du cancer du poumon, que 75 % des malades sont des fumeurs et également que 60 % des français sont des fumeurs.
Soit A l'événement "être atteint du cancer" et B l'événement "être fumeur".
On a P(B | A) = 0.75 ,
P( A ) = 0.04 ,
P( B ) = 0.6.
D'où P(A ∩ B) = P( A ) P(B | A) = 0.04 × 0.75 = 0.03 (probabilité d'être atteint de la maladie et fumeur)
P(A | B) = 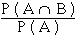 =
= 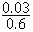 = 0.05 (probabilité d'être atteint du cancer quand on est fumeur)
= 0.05 (probabilité d'être atteint du cancer quand on est fumeur)
P(A | 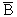 )
=
)
= 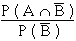
P( 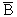 ) = 1 - P( B ) = 1 - 0.6 = 0.4
) = 1 - P( B ) = 1 - 0.6 = 0.4
P(A ∩ 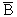 )
= P( A ) - P(A ∩ B) = 0.04 - 0.03 = 0.01
)
= P( A ) - P(A ∩ B) = 0.04 - 0.03 = 0.01
D'où P(A | 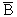 ) =
) = 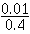 = 0.025
= 0.025
Soit E une expérience aléatoire et A un événement lié à cette expérience aléatoire. A est une assertion qui peut être vraie ou fausse à la suite d'une épreuve de E . Si A est vraie à la suite d'une épreuve de E , on dit que A s'est réalisé ou qu'on a assisté à une réalisation de A.
Exemple : Si E est l'expérience aléatoire consistant à lancer un dé, et dont les issues sont les nombres qui apparaissent sur la face supérieure du dé après immobilisation.
Soit A l'événement "le numéro est pair". On lance le dé. Le numéro obtenu est 4 : l'événement A s'est réalisé. On dit aussi qu'on a assisté à une réalisation de A.
Si X et Y sont deux ensembles disjoints : X ∩ Y = ∅
card(X ∪ Y) = card( X ) + card( Y )
Exemple : Un enfant a 4 voitures miniatures rouges et 3 voitures miniatures vertes.
Il a en tout 7 = 3 + 4 voitures miniatures.
Si X1 , X2 , ... , Xn sont n ensembles deux à deux disjoints, c'est-à-dire si :
Xi ∩ Xj = ∅ pour i ≠ j
card( X1
∪ X2
∪ ... ∪ Xn )
= ![]() card( Xi )
card( Xi )
Soit X un ensemble.
A1 , A2 , ... , An une partition de X.
Si chaque classe Ai a le même nombre p d'éléments :
card( X ) = np
Exemple : Un restaurant a commandé 1 200 bouteilles de vin, qui lui sont expédiées par carton de 12 bouteilles.
1 200 = 12 × 100
100 cartons sont nécessaires pour effectuer l'expédition. On les numérote de 1 à 100. Si Ai constitue l'ensemble des bouteilles contenues dans le ième carton, A1, A2 , ... , A100 est une partition de l'ensemble X des bouteilles expédiées ; chaque classe Ai ayant le même nombre d'éléments, à savoir 12.
Soit X et Y deux ensembles non vides.
L'ensemble des couples ordonnés ( x , y ) où x ∈ X ,y ∈ Y, constituent l'ensemble produit X × Y
card(X × Y) = card( X ) card( Y ) (Règle du produit)
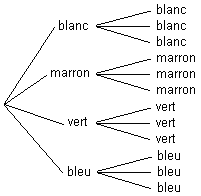
Les éléments de X × Y peuvent s'obtenir à l'aide d'arborescences.
Exemple : Un marchand de réfrigérateurs propose un modèle en quatre coloris : blanc, marron, vert, bleu et en trois dimensions :
X = { blanc, marron, vert, bleu }
Y = {1.10, 1.20, 1.30}
X × Y représente les choix possibles dans ce modèle
card(X × Y) = card( X ) card( Y ) = 3 × 4 = 12
On obtient tous les éléments de X × Y par une arborescence.
Soit X un ensemble. A et B deux parties de X. On appelle réunion ou union des deux parties A et B, la partie notée A ∪ B de X, constituée des x ∈ X, tels que x ∈ A ou x ∈ B.
Système complet d'événements :
Soit Ω l'ensemble des issues d'une expérience aléatoire E;
A1 , A2 , ... , An n événements liés à l'expérience E. On dit que les événements A1 , A2 , ... , An constituent un système complet d'événements
1) s'ils sont deux à deux incompatibles
2) si leur réunion est l'événement certain Ω
Ap ∩ Aq = ∅ si p ≠ q
A1 ∪ A2 ∪ ... ∪ An
= Ω
On appelle univers des possibles d'une expérience aléatoire, l'ensemble Ω des issues de cette expérience.
Exemple : Si on lance une pièce de monnaie, l'univers des possibles a deux éléments P ou F :
P correspondant à la pièce retombe sur pile
F correspondant à la pièce retombe sur face
Ω = { F, P }