LEXIQUE :

Centiles :

Les centiles d'une variable aléatoire continue X, de fonction de répartition F, sont les nombres x₁, x₂ , ... , x₉₉ tels que :

F ( x₁ ) = 0.01 ; F ( x₂ ) = 0.02 ; ... F ( x₉₉ ) = 0.99.

Autrement dit, x₁ est tel que la probabilité d'avoir X inférieur à x₁ est la même que celle d'avoir X compris entre x₁ et x₂, et que celle d'avoir X compris entre x₂ et x₃, etc...

Cette probabilité vaut 0.01.

Centrée :

On dit qu'une variable aléatoire X est centrée (ou que sa loi est centrée) si son espérance est nulle : E ( X ) = 0.

On dit que l'on centre une variable aléatoire X quand on lui ôte sa moyenne : X - E ( X ) est une variable centrée.

Si X n'est pas constante, 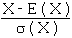est une variable centrée réduite.

Coefficient de corrélation :

Coefficient de corrélation linéaire entre deux variables numériques:

σ ( X , Y ) =

Ce nombre est toujours compris entre -1 et +1. Il est égal à ± 1 quand il existe une relation entre X et Y de la forme Y = a X + b.

Si X et Y sont indépendantes, il est nul.

Si σ ( X , Y ) = 0, on dit que X et Y sont non corrélées.

Convergence :

a) de la loi binomiale vers la loi de Poisson :

Si X suit B ( n , p ) , n → ∞ , p → 0, np → λ , alors la loi de X se rapproche de P ( λ ) .

(en pratique, si n > 50 et p < 0.1, on peut remplacer B ( n , p )
par P ( n p ) )

b) de la loi binomiale vers la loi normale :

Si X suit B ( n , p ), quand n → ∞, 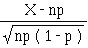tend vers
la loi N ( 0 , 1 ).

(en pratique, si np > 18 et p assez proche de 0.5, on peut remplacer la loi de X par N ( n p , )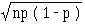

c) de la loi de Poisson vers la loi normale :

Si X suit P( λ ), 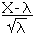tend, quand λ → ∞, vers la loi N ( 0 , 1 )

(en pratique, si λ > 18, on peut remplacer la loi de X par N ( λ, ))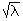

Couple de variables aléatoires :

C'est l'ensemble de deux variables aléatoires définies sur le même univers Ω.

Si X prend ses valeurs sur et Y sur 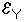, le couple ( X , Y ) est à valeurs sur × .

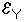Exemple : dans l'épreuve consistant à tirer au hasard une carte dans un jeu, on peut définir X comme étant la couleur de la carte, et Y sa valeur :

= { trèfle, carreau, coeur, pique }

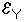= { 2, 3, ..., 10, valet, dame, roi, as }

Covariance :

Covariance entre deux variables aléatoires numériques :

cov( X , Y ) = E [ ( X - E ( X )) ( Y - E ( Y ))] = E ( X Y ) - E ( X ) E ( Y )

Si X et Y sont indépendantes, leur covariance est nulle (la réciproque est fausse)

Déciles :

Les déciles d'une variable aléatoire continue X, de fonction de répartition F, sont les nombres x₁ , x₂ , ... , x₉ tels que
F ( x₁ ) = 0.1 ; F ( x₂ ) = 0.2 ; ... F ( x₉ ) = 0.9.

Autrement dit x₁ est tel que la probabilité d'avoir X inférieur à x₁ est la même que celle d'avoir X compris entre x₁ et x₂ et que celle d'avoir X compris entre x₂ et x₃, etc...

Cette probabilité vaut 0.1.

Ecart-type :

L'écart-type d'une variable aléatoire numérique X, noté σ ( X ), est la racine carrée de la variance.

L'écart-type s'exprime dans la même unité que X ; c'est un nombre positif ou nul, nul si X est une constante, et d'autant plus grand que les valeurs de X sont "imprévisibles".

Exemple : si X suit une loi normale, la probabilité pour que X soit compris entre E ( X ) - 2 σ ( X ) et E ( X ) + 2 σ ( X ) est à peu près de 0.95.

Ensemble dénombrable :

C'est un ensemble fini ou infini de valeurs numériques, que l'on peut énumérer.

Exemple :

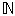= {0,1,2,3,4,5,...}, ou l'ensemble des nombres impairs {1,3,5,7,...}, ou l'ensemble des multiples de 5 supérieurs à 10 {15,20,25,30,...} sont des ensembles infinis dénombrables.

Par contre, les intervalles réels de la forme [ a , b ] ,
ou par exemple { x / x > a } sont infinis mais non dénombrables.

Espérance :

L'espérance (mathématique) d'une variable aléatoire numérique X, appelée aussi parfois par abus de langage moyenne de X, est la valeur que l'on peut espérer obtenir, en moyenne, en réalisant X.
Elle est notée E ( X ).

a) dans le cas d'une variable X discrète, de loi de probabilité définie par les x_i et les p_i, c'est la moyenne des x_i, pondérée par les p_i

E ( X ) = ∑ ( x_i p_i )

b) dans le cas d'une variable X continue, de fonction de densité f, c'est l'intégrale, sur l'intervalle des valeurs de X, de la fonction x f ( x ) :

E ( X ) = ∫ x f ( x ) dx

Espérance conditionnelle :

L'espérance conditionnelle de X, sachant Y = y est l'espérance de la loi conditionnelle :

E ( X / Y = y_j ) = 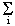x_i 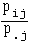dans le cas discret

E ( X / Y = y ) = ∫ x 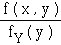d x dans le cas continu.

C'est la valeur que l'on peut espérer obtenir en moyenne pour X, lorsque Y prend une valeur donnée.

Fonction de densité :

La fonction de densité f_X d'une variable aléatoire continue X est la dérivée de sa fonction de répartition. C'est une fonction positive ou nulle, telle que son intégrale sur 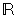(aire comprise entre la courbe représentative de f_X et l'axe des abscisses) est égale à 1.

La probabilité pour X d'être dans un intervalle [ a , b ] (ouvert ou fermé, éventuellement infini) se calcule par l'intégrale de f_X sur cet intervalle, c'est-à-dire l'aire délimitée par la courbe représentative de f_X, l'axe des abscisses et les verticales d'abscisses a et b.

Fonction de répartition :

La fonction de répartition d'une variable aléatoire numérique X est une fonction réelle F qui, à tout x de 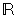, associe la probabilité d'obtenir pour X une valeur inférieure ou égale à x :

F ( x ) = P ( X ≤ x )

F est une fonction croissante de 0 à 1.

- si X est discrète, F est une fonction en "escalier" (c'est-à-dire constante par morceaux). Ses valeurs s'obtiennent en cumulant les probabilités élémentaires p_i = P ( X = x_i ) , et les valeurs x_i de sont les abscisses des points de discontinuité de X.

- si X est continue, F est une fonction continue, croissant de 0 à 1 sur l'intervalle des valeurs de X. Sa dérivée est alors la fonction de densité de X.

Fonction de répartition empirique :

Fonction réelle calculée sur un échantillon de taille n qui, à tout réel x, associe la proportion d'éléments de l'échantillon ≤ x.

Par exemple F ( x ) peut être le % d'ampoules de durée de vie inférieure ou égale à x, sur un échantillon de 500 ampoules.

(Alors que la fonction de répartition théorique de la durée de vie d'une ampoule de ce type est la probabilité que sa durée de vie soit inférieure ou égale à x).

Indépendance :

Deux variables aléatoires X et Y sont indépendantes si la connaissance de la réalisation d'un événement lié à l'une des deux ne modifie pas les probabilités d'événements liés à l'autre.

a) Si X et Y sont discrètes, elles sont indépendantes si et seulement si
P ( X = x_i et Y = y_j ) = P ( X = x_i ) . P ( Y = y_j ), pour tout x_i de et tout y_j de .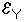

b) Si X et Y sont continues, elles sont indépendantes si et seulement si la fonction de densité du couple ( X , Y ) est le produit des densités marginales.

Loi binomiale :

C'est la loi de X = nombre de réalisations d'un événement dans une suite de n épreuves indépendantes où l'événement a la probabilité p de se produire.

X est la somme de n variables de Bernoulli indépendantes de même p :

= { 0 , 1 , 2 , ... , n } , P ( X = k ) = 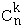p^k (1 - p)^n-k ,
∀ k ∈ { 0 , 1 , 2 , ... , n }

Exemples :
nombre de "pile" obtenu en lançant 10 fois une pièce : B (10 ; 0,5)
nombre de pièces défectueuses trouvées parmi 100 ...

Loi conditionnelle :

. Si ( X , Y ) est un couple de variables discrètes, la loi conditionnelle de X, sachant Y = y_j, est la loi définie sur par

P ( X = x_i / Y = y_j ) =

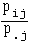
. De même, les P ( Y = y_j / X = x_i ) = 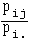définissent sur 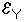la loi conditionnelle Y, sachant X = x_i.

. Si ( X , Y ) est un couple de variables continues, de densité conjointe f, la loi conditionnelle de Y sachant que X = x (où x est tel que f_X ( x ) ≠ 0 ) a pour densité .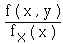

De même, si f_Y( y ) ≠ 0, la densité conditionnelle de X, sachant Y = y, est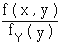

Loi conjointe :

C'est la loi d'un couple de variables aléatoires ( X , Y )

a) Si X et Y sont discrètes, elle est définie par les
p_ij = P ( X = x_j et Y = y_j ) , nombres ≥ 0 de somme 1, définissant une probabilité sur ×

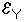
b) Si X et Y sont continues, elle est définie par la densité conjointe
f ( x , y ) , fonction ≥ 0 sur 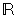² , d'intégrale 1, telle que

P ( a < X < b et c < Y < d ) = 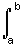[ 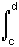f ( x , y ) d y ] d x

Loi de Bernoulli :

C'est la loi d'une variable aléatoire X prenant les valeurs 1 et 0 avec les probabilités :

Exemple : tirer à "pile ou face", tester une pièce dans la production d'une machine (pièce défectueuse ou pas), ...

Loi de Poisson :

C'est la loi d'une variable X à valeurs dans N telle que
P ( X = k ) = 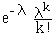, k ∈ N

Si X suit une loi binomiale B ( n , p ) avec p faible ( < 0, 1 ),
et n grand ( n > 50 ), la loi de X est très proche de la loi P ( n p ).

Exemple : nombre de pièces défectueuses dans un grand échantillon de bonne qualité.

C'est aussi la loi du nombre d'événements se produisant pendant une période T, ou sur une distance T, et ne dépendant que de T, les événements étant indépendants, et non simultanés.

Exemple : nombre d'accidents par an sur une route, nombre de défauts par mètre de tissu, nombre d'appels téléphoniques reçus à un standard pendant une journée.

Si X suit une loi P ( λ ), E ( X ) = V ( X ) = λ

Loi de probabilité : ( ou distribution )

La loi de probabilité, ou distribution, d'une variable aléatoire X est définie par l'ensemble des valeurs prises par X, et la probabilité P_X définie sur :

- dans le cas d'une variable discrète ou d'une variable qualitative par les
p_i = P ( X = x_i ) ; les x_i étant les éléments de , et les p_i les probabilités pour X de prendre ces valeurs .

Ces p_i sont des nombres positifs ou nuls, de somme égale à 1. La distribution de X peut être représentée par un diagramme en bâtons.

- dans le cas d'une variable continue : par la fonction de densité de X, f_X, dérivée de la fonction de répartition.

C'est une fonction positive ou nulle, telle que son intégrale sur 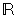(aire comprise entre la courbe représentative de f_X et l'axe des abscisses) est égale à 1.

Loi exponentielle :

X est une variable aléatoire de loi exponentielle de paramètre λ (nombre réel > 0) si sa densité est :

Sa fonction de répartition est :

Cette loi se rencontre fréquemment comme durée de vie d'un matériel qui ne vieillit pas.

Loi géométrique :

C'est la loi du nombre X d'épreuves indépendantes à réaliser pour voir apparaître pour la première fois un événement de probabilité p:

Exemple : nombre de lancers d'un dé jusqu'à obtention de "6"
nombre de pièces à tester pour trouver la première défectueuse
nombre de tentatives pour avoir le 1^er succès, etc...

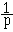E ( X ) =     ,       V ( X ) =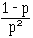

Loi hypergéométrique :

C'est la loi du nombre X d'individus possédant un certain caractère, lors du tirage sans remise de m individus parmi n, dont une certaine proportion p a ce caractère :

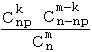P ( X = k ) =     ,       k ∈ { 0, 1, 2 , ... , m }

(si le tirage s'effectue avec remise, X suit une loi binomiale
B ( m , p ) )

Si n est grand ( m / n < 0,1), la loi de X est à peu près B ( m , p ).

Loi marginale :

C'est la loi de probabilité d'une variable X (ou d'une variable Y) obtenue à partir de la loi du couple ( X , Y ).

. S'il s'agit de variables discrètes, les lois marginales s'obtiennent par :

p_i. = P ( X = x_i ) = p_ij

p_.j = P ( Y = y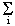_j ) = p_ij

. S'il s'agit de variables continues, les densités marginales s'obtiennent par :

f_X ( x ) = ∫ f ( x , y ) d y

f_Y ( y ) = ∫ f ( x , y ) d x

Loi normale : Loi de Laplace-Gauss

a) X suit une loi normale centrée réduite, notée N ( 0 , 1 ), si sa fonction de densité est :

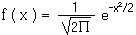
Sa fonction de répartition se lit dans une table.

b) X suit une loi normale de paramètres m et σ , noté N( m , σ ), si sa fonction de densité est :

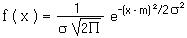
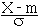suit alors une loi normale centrée réduite.

On dit aussi que X suit une loi de Gauss ou une loi de Laplace-Gauss.

Loi uniforme continue :

X est une variable aléatoire de loi uniforme sur un intervalle [ a , b ] si sa fonction de densité est constante sur cet intervalle :

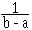f ( x ) = si x ∈ [ a , b ]     ,       f ( x ) = 0 si x ∉ [ a , b ]

La probabilité pour que X appartienne à un intervalle contenu dans [ a , b ] est proportionnelle à la longueur de cet intervalle.

Loi uniforme discrète :

C'est la loi d'une variable aléatoire X prenant les valeurs { 1 , 2 , ... , n } avec des probabilités égales :

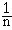P ( X = k ) =     ,       ∀ k ∈ { 1 , 2 , ... , n }

Exemple : point obtenu en lançant un dé, loterie à 1 000 numéros successifs, ...

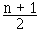E ( X ) =     ,       V ( X ) =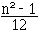

Médiane :

La médiane d'une variable aléatoire continue X de fonction de répartition F, est le nombre x tel que F ( x ) = 1/2.

Autrement dit, x est tel que la probabilité d'avoir X inférieur à x est la même que celle d'avoir X supérieur à x, c'est-à-dire 1/2.

Modalités :

Les modalités (ou catégories) d'une variable aléatoire qualitative sont les différentes valeurs que peut prendre cette variable.

Exemple :

à l'épreuve aléatoire qui consiste à choisir un individu au hasard dans une population, on peut associer la variable aléatoire qualitative "couleur des cheveux", dont les modalités sont : blond, roux, noir, châtain, blanc.

Quartiles :

Les quartiles d'une variable aléatoire continue X, de fonction de répartition F, sont les nombres q₁, q₂, q₃ tels que :

Autrement dit, q₁ est tel que la probabilité d'avoir X inférieur à q₁ est la même que celle d'avoir X compris entre q₁ et q₂, la même que celle d'avoir X compris entre q₂ et q₃, et la même que celle d'avoir X supérieur à q₃.

Cette probabilité vaut 0.25.

Le deuxième quartile q₂ est égal à la médiane.

Réduite :

On dit qu'une variable aléatoire X est réduite (ou que sa loi est réduite) si sa variance est égale à 1 (et donc son écart-type aussi) : V ( X ) = 1

On dit que l'on réduit une variable aléatoire X (non constante) quand on la divise par son écart-type :

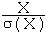  est une variable réduite,

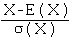  est une variable centrée réduite.

Tchébichev : Inégalité de (Bienaymé)-Tchébichev

Si X est une variable aléatoire numérique, d'espérance E ( X ), et d'écart-type σ ( X ), on a, pour toute constante t positive,

P ( | X - E ( X ) | < t σ ( X ) ) > 1 - 1/ t²

Exemple : avec t = 2, cette inégalité signifie que la probabilité pour que X soit compris entre E ( X ) - 2 σ ( X ) et E ( X ) + 2 σ ( X ) est supérieure à 0.75, quelle que soit la "forme" de la distribution de X.

Théorème central limite :

Si X₁, X₂, X₃ , ... , X_n sont des variables aléatoires indépendantes, de même loi de probabilité, d'espérance µ et de variance σ², la loi de probabilité de

tend, quand n → ∝, vers la loi normale centrée réduite.

Variable aléatoire :

Une variable aléatoire X est une grandeur qui peut prendre différentes valeurs avec différentes probabilités ; l'ensemble des valeurs que peut prendre X est noté .

X est en fait une application qui, à toute issue d'une expérience aléatoire, associe un élément de .

Selon la nature de , X sera une variable qualitative, numérique discrète ou numérique continue.

Variable aléatoire continue :

Une variable aléatoire X est continue si l'ensemble des valeurs qu'elle peut prendre est 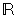ou un intervalle réel. Il s'agit donc d'un ensemble infini non dénombrable : on ne peut pas énumérer systématiquement l'ensemble de tous les points d'un intervalle réel.

Exemple :

X peut être l'âge d'une personne prise au hasard, ou sa taille, ou son poids. Si celui-ci est exprimé en kgs, on peut raisonnablement penser que est un intervalle compris dans [ 0 , 500 ].

Variable aléatoire discrète :

Une variable aléatoire X est discrète si l'ensemble des valeurs qu'elle peut prendre est un ensemble numérique fini (c'est-à-dire comprenant un nombre fini d'éléments) ou un ensemble infini dénombrable (c'est-à-dire comprenant une infinité de nombres que l'on peut énumérer).

Exemple :

X peut être le point obtenu en lançant un dé à 6 faces ,
avec = {1,2,3,4,5,6}, ou bien le nombre de lancers nécessaires pour obtenir un 6, avec = {1,2,3,...}, ensemble infini.

Variable aléatoire numérique : (ou réelle)

Une variable aléatoire X est numérique (ou réelle) si l'ensemble des valeurs qu'elle peut prendre est un ensemble de nombres, fini ou infini, ou un intervalle de valeurs réelles, éventuellement 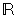entier. Selon la nature de , X sera dite discrète ou continue.

Exemples :

X peut être le point obtenu en lançant un dé à 6 faces,
avec = {1,2,3,4,5,6}, ou le nombre de lancers nécessaires pour obtenir un 6, avec = {1,2,3,...}, ensemble infini.

X peut être l'âge d'une personne prise au hasard, ou sa taille, ou son poids. Si celui-ci est exprimé en kgs, on peut raisonnablement penser que est un intervalle compris dans [ 0 , 500 ].

Variable qualitative :

Une variable aléatoire X est qualitative si l'ensemble des valeurs qu'elle peut prendre est qualitatif, c'est-à-dire non numérique.

Exemples :

X peut être la couleur obtenue en tirant une carte au hasard dans un jeu de 32 cartes,

X peut être la couleur des yeux d'une personne prise au hasard, ou sa région de naissance, ou sa catégorie socio-professionnelle, etc ...

Variance :

La variance d'une variable aléatoire numérique X, notée V ( X ), est un nombre positif ou nul, nul si X est une constante, et d'autant plus grand que les valeurs de X sont "imprévisibles".

V ( X ) = E [ ( X - E ( X ) )² ] (ici E signifie l'espérance)

On a aussi : V ( X ) = E ( X² ) - [ E ( X ) ]², formule qui peut se lire : la variance est égale à l'espérance du carré moins le carré de l'espérance.

La racine carrée de la variance est l'écart-type.